Week 7: Quiz review

We've continued practicing proofs in the lectures. This week, I would like to review the quiz #4 because I realized that I missed important thing. Quiz #4 was writing a proof statement for the given statement.

When you show the statement is true/false, you pick a number for the part of the proof. (Ex. x, y, z). In the main part of the proof, a number I picked should be expressed as a different number from the one in the original statement. If the number's symbol was x, then I should use the number, for example, x' to indicate that this is different number. Then, when I conclude, I can use the original symbol to generalize. The below is the given statement in quiz #4.

                             

So, basically, to prove the above statement, in the process of proving, I should have used other related symbol instead of z in the original statement. If it wasn't this quiz, I probably wouldn't realize and keep doing in a wrong way in my proof.  Now, the following is the proof that I rewrote with 'the correct' symbols.



Assume x and y are real numbers.  # x, y are typical generic real numbers.
    Assume x  >  y.         # antecedent.
        Let z is a real number.    # def'n of z'. z' is a real number st x > z and x > y.
            Then, x > z'.
              .
              .
              .
              # Prove there is z' satisfies x > z'.
              .
              .
              Then, z' > y.
              .
              .
              .
              # Prove there is z' satisfies z' > y.
              .
              .
              Then, x  > z and z' > y # by previous proofs.
        Then,    # since we assumed z s a real number.
    Then,   # since we assumed x > y. we got this conclusion.
Then,   # we assumed generic real                                                                                                                        # numbers x, y.





Sorry for the unmatched line in the last three steps of my proofs! I tried to match the line, but since I copied the equation as a picture, the size won't change. I tried to type the whole proof using LaTex but it wasn't pretty in the end. Anyway, the bottom line is that now I remember for sure to use different symbols in my main part of proof!

Week 6: Proofs

The class continued how to write proofs with some different conditions such as proving inequality, existence, a sequence, non-boolean functions, using definition, proof by cases...We studied all these different cases but the structure of the proofs were basically same.

You start with the general assumption.

ex) Assume that n is generic natural number.

And then, use indentation on the next line in order to start an assumption under the initial assumption. You prove the process one in each line. At the end of each line, put '#' symbol and justify your process all the time. These assumption also need an indentation under the assumption. When you reached the last process, write the conclusion for the last assumption with the same position as the starting of the last assumption. Same thing with the other assumptions and conclusions.

ex)

Assume that n is generic natural number.

    Assume that...... #explain why

        Then, prove 1... #justify this proof

        Then, prove 2... #justify this proof

        .

        .

        .

        .

    Then, ...(conclusion), since assumed that... #assume that.....got (conclusion)

Then,......(complete conclusion), because n is generic natural number.

Above is the general format of proving example. This actually reminded me of  function recipe in python. When you write a body of function definition, if we use if, for, while, etc., we have to put an indentation on the next line which is the content of those. And when it's finished and return something, unindent the line back. I understood the format of proving, but if I don't know how to prove things, it wouldn't matter. So I guess the important thing is that I practice 'how to show that something is true\false'.

Week 5: Continued proving and Mid-term exam!

This week we had the first mid-term exam. Yes! Mid-term exam. For me, it was the very first exam since I start at U of T. I was very worried that the exam might be too hard so there's question which I can't even solve. It turned out that it wasn't a 'super-hard-I-have-no-idea' exam. Actually, I was surprised at resemblance of previous session's exam.

Before the exam, I went over all my notes, and practice tutorials, quizzes, assignment and the old exam that professor posted. I kept doing again because somehow, I felt like I have a different answer every time I tried the questions. That actually why I was so worried. I wasn't sure if I am capable of doing logic in a right way.

Since the test allowed to bring a piece of paper that I can write anything that I wanted. At first, I thought about taking some notes with me. But I decided not to take anything with me and just take the test. I thought, if I still didn't understand and don't know something until the moment I take a test, that means, I don't know. The fact that I still needs some memo on how to interpret something into logic means I still don't understand the concepts, so even though I have aids with me, that won't really help. I mean, even if I had a help sheet, when I look at the questions, if I have no idea what is going on there, then it doesn't matter if I have a help sheet or not. I simply don't know. That's why I didn't bring any help sheet with me.

Anyway, the test didn't really need any help sheet. First  two questions were same type as the previous session's exam and the last one was similar to the one in the  assignment 1 problem. I don't know if I received good marks, but I am just glad I was able to finish all the problems on time. (Although, we kind of went over the solution on Friday lecture, I don't quite want to think about the exam since I still have the other exams to take...)

Week 4: Mixed quantifiers, proof

In week 4, we continued with symbols and quantifiers as well as starting with proof. As previously mentioned, what we are learning in this course is same as what we learned in Calculus! course during the first and the second week.

To show that the order of quantifiers cannot be switched, there was an example with the definition of limit.

The definition says that 'for all epsilon, there exist some deltas', means if I choose any epsilon, I can always find delta. But can we choose delta first(switch the order of quantifiers)? No, it will not work. If I pick a specific delta first, then my enemy can choose any delta that is out of range of delta. Than, the definition is not working anymore. Therefore, we know that the order of quantifiers matters regarding to the truth of implications. 

This is, although, not always true. There are some cases that implication is not affected by the order of quantifiers. When quantifiers are elements of an ordered pair, it does not change anything. For example, below are same:

When I prove something, first, I have to convince myself why this is true. In other words, I have to understand why this is true and need to have an idea about proving steps. Next step is writing down the steps of proving. When I prove something, I have to justify my thought to convince other people who will read my proof. If I find any defects in the process, I may go back to the beginning.

Now I recall the type of proofs that I learned in Calculus! course. There are four types of proofs.

• Direct proof
• Proof by contrapositive
• Proof by contradiction
• Proof by induction

In Calculus! course, proof by induction was focused. Mathematical induction is used to prove a property holds for any natural integer. If we want to prove P(n) is true, then we assume the P(1) is true and show that if P(n) is true then P(n+1) is also true. 

In CS, we start with direct proof. Most of the time, direct proof can be a very hard way to prove, When, prove directly, show each link to reach to the precedents. When we prove something like,

 

we use following structure:

    Assume x is in X.

        Assume P(x).

            Then, R1(x)

            C2.0 for all x in X, P(x) then R1(x)

            Then, R2(x)

            C2.1 for all x in X, P(x) then R2(x)

             ...

        

            C2.n for all x in X, P(x) then Rn(x)

        Then P(x) then Q(x)

    Then for all x in X, if P(x) then Q(x)

Indentation indicates scope of assumption. This reminds me of writing definition in Python. When we write definition in Python, indentation is very important. For example, when we use if statement in the function body, if indentations is not adequate, the function is not working properly. 

This way of proving is slightly different from math, so it was little uncomfortable for me to use(For example, indentation). 

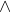
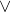
For this week, I remember one thing very well: chains with  or . It is because of the tutorial problem. In one of the tutorial problems, there was a question asking to write a given statement symbolically. The statement is 'A and B are both guarantees that C is true.' Actually, my answer was wrong. My answer was,

, which is not quite right. After I read this part, I could understand why my answer in not right. 

Let's write the statement in symbols again. It would be

Now, following implications are equivalent to the above:

(By the rules for manipulating predicates)

Therefore, 

At the time of tutorial, I didn't know what I did wrong, but after the lecture, I tried applying those rules by myself and I could understand and solve the problem.