I feel really stuck. Over the last 2 weeks, I've reviewed, studied Big-O and Omega. I went over the lecture slides, lecture note and practice on my own repeatedly, reviewed tutorials and quizzes. And I finally know how to do it. But this time, I think I am really stuck. I am really worried that I might not be able to do this even until the exam.(Hope that doesn't happen!)
It was the hardest last two weeks for me because the contents felt really hard and I barely understood material. Unfortunately, the last tutorial wasn't about computability or halt. Usually, when I'm stuck, tutorials were really helpful. I would understand the material after the tutorials so it really helped me to keep going and studying. I was hoping to deal with some of these problems on the last tutorial, but we did more of Big-O and Omega.
In terms of terminology, if the function f is well-defined function, that is we can say what f(x) is for every x, but we can't say how to compute f(x), then f is non-computable. As an example, we were introduced to the function halt as a non-computable function. Also, in order to prove uncomputable function, we use reductions.
Suppose that we know some function f is non-computable, the some other well-defined function g could be extended to build f. In other words:
If g is computable, then f is computable.
Using the contrapositive, f reduces to g:
If f is non-computable, then g is non-computable.
Unfortunately, I haven't fully understood about halt and the process of proving some function's computability so I don't think I can go further than this. I mean, I did sort of copy lecture note for Q6 in Assignment #3, but I'm not confident about this at all because I basically am not really understanding this. It feels bad that I could not make this SLOG with better understanding. But I will keep trying until the exam and get help if I really can't figure out by my self.( I usually prefer try by myself as much as possible cause in that case, it feels so much better and the contents actually last longer in my head..I think.) So, I guess at least I know what I have to do. review the slides and the lecture notes over and over until I understand and practice and practice until I get close to perfect.
Search This Blog
Sunday, November 30, 2014
Sunday, November 16, 2014
Week 10: Linear search and Big-O
At last part of the lecture, we learned about analyzing algorithm. For the given Python code, we analysed(counted) the number of execution time for each assignment statement. Why do we do that? Why do we analyse how many steps there are in the code, what the total steps are, etc.? The answer is to measure the running time of the programs.
For example,
def LS(A, x):
""" Return an index i such that x == L[i]. Otherwise, return -1."""
i = 0
while i < len(A):
if A[i] == x:
return i
i = i + 1
return -1
if we consider the code like this, with few example such as LS([2, 4, 6, 8], 4) we can find the running time of the program. This could be the example of linear search. This part overlaps CSC108 contents. Linear search can be meant 'arranged in line'. And there is binary search. Binary algorithm is much faster than linear search because binary search requires the list to be sorted. (when sorted the list, if the list already sorted, there will be nothing to sort!) For example, if we use linear search on one billion items, there will be one billion iterations in the worst case(literally going through one billion items), however, with binary search, it only requires 30 iterations in the worst case. Now, we see the difference.
Now, it's time for Big-O, Omega and Theta come along. Why do we care these? These are the expression of how the established linear or binary search graph behaves when n is 'large enough'.
To be precise, the definition of Big-O is the same as the following.
For any function f : N → R≥0
O(f) = {g:N → R≥0|∃c ∈ R+, ∃B ∈ N, ∀n ∈ N, n ≥ B ⇒ g(n) ≤ cf(n)}
So means that f grows faster than g, or f is an upper bound for g. For Omega, it will be the other way, for Theta, g is bounded on both.
means that f grows faster than g, or f is an upper bound for g. For Omega, it will be the other way, for Theta, g is bounded on both.
For example,
def LS(A, x):
""" Return an index i such that x == L[i]. Otherwise, return -1."""
i = 0
while i < len(A):
if A[i] == x:
return i
i = i + 1
return -1
if we consider the code like this, with few example such as LS([2, 4, 6, 8], 4) we can find the running time of the program. This could be the example of linear search. This part overlaps CSC108 contents. Linear search can be meant 'arranged in line'. And there is binary search. Binary algorithm is much faster than linear search because binary search requires the list to be sorted. (when sorted the list, if the list already sorted, there will be nothing to sort!) For example, if we use linear search on one billion items, there will be one billion iterations in the worst case(literally going through one billion items), however, with binary search, it only requires 30 iterations in the worst case. Now, we see the difference.
Now, it's time for Big-O, Omega and Theta come along. Why do we care these? These are the expression of how the established linear or binary search graph behaves when n is 'large enough'.
To be precise, the definition of Big-O is the same as the following.
For any function f : N → R≥0
O(f) = {g:N → R≥0|∃c ∈ R+, ∃B ∈ N, ∀n ∈ N, n ≥ B ⇒ g(n) ≤ cf(n)}
So
Sunday, November 9, 2014
Week 8 & 9: Proving negation, Algorithm Analysis(2)
We've been taught about algorithm analysis for about 2 weeks now.(oh my Big O! *face-palm*) I honestly had no idea what we were doing for a couple of lectures at the beginning of this. I guess, I wasn't connecting the proofs of big O, etc to the algorithm that we analyzed on the first day of algorithm analysis. I had lost during that time, because I didn't know from where the big O and all the proving stuff came out all of sudden.
After the time of chaos in my head, after the tutorial time and reviewing the material, something clicked and I finally made 'Ah!' sound.
The start is find out the what the given code means. Once I understand the code, count the number of execution of each line of codes. If it is not easy to generalize at once, start from the small number and see how many times each line is executed and do this for several times. Then generalize from the results. (While I'm practicing this with tutorial problem and lecture material, I got little confused at some point and lost the track of count......means that I forgot if I count this line at that point already or if I'm about to count.....duh...)
Proving still feels difficult for me. At this point, the proof style requires that we choose any existential and make the given equation simpler format(like finding bigger possible number, etc). I definitely need more practice on this. When Danny is doing this together in the lecture, I can follow what we are doing, but I am not confident to do this all by myself from the beginning. I know only the practice makes it perfect, so I guess that's what I will do and hopefully, by next week, I can understand this fully and write the proofs fairly well.
After the time of chaos in my head, after the tutorial time and reviewing the material, something clicked and I finally made 'Ah!' sound.
The start is find out the what the given code means. Once I understand the code, count the number of execution of each line of codes. If it is not easy to generalize at once, start from the small number and see how many times each line is executed and do this for several times. Then generalize from the results. (While I'm practicing this with tutorial problem and lecture material, I got little confused at some point and lost the track of count......means that I forgot if I count this line at that point already or if I'm about to count.....duh...)
Proving still feels difficult for me. At this point, the proof style requires that we choose any existential and make the given equation simpler format(like finding bigger possible number, etc). I definitely need more practice on this. When Danny is doing this together in the lecture, I can follow what we are doing, but I am not confident to do this all by myself from the beginning. I know only the practice makes it perfect, so I guess that's what I will do and hopefully, by next week, I can understand this fully and write the proofs fairly well.
Week 8 & 9: Proving negation, Algorithm Analysis
Quizzes always make me nervous. Well, what wouldn't make me nervous if it is graded, but the thing about the quizzes is that it comes back every week. It is a bit pressure sometimes, but there is an advantage of taking quizzes as well. The good thing about taking quizzes that I found is that it is the opportunity to test myself if I studied material correctly. The given problem for each quiz is asking fairly basic concept of what we learned in previous week. What I learned from quizzes actually helped me in Assignment #2.
Again(I wrote about quiz last week as well), I got quiz #6 wrong. I think I was misunderstanding about proving negation or didn't apply disproving the statement by proving negation flexibly.
Suppose there is a statement that you should prove or disprove. Let's say, after the brainstorming in my head, if I figured out that the given statement is false so I have to disprove it. When disprove the statement, most of the times you negate the given statement and try to find a counterexample. If I can show a counterexample, then that is enough to prove the negation is true. If I show the negation is true, then the original statement is disproved.
Here is the statement from Quiz #6:
For all real numbers x, y, if x and y are both positive, then
Now, I want to disprove this statement, so I found the negation and showed there exists a counterexample.

Let . Then
. Then 
Let . Then
. Then  .
.
Notice, . #
. # 
Then, . # algebra
. # algebra
Then, . # algebra
. # algebra
Therefore,
Thus, .
.
Note that we don't need to indent anything when you show that there is a counterexample. You indent the next proof line only when you assume something. But in this case, showing negation is true, we only introduce there exists a counterexample, so we can write the each step without any indentation.
After this quiz, I realized that I didn't write some of my proofs in assignment #2. Thanks to the quiz, I could handed in the right format of proofs.
Again(I wrote about quiz last week as well), I got quiz #6 wrong. I think I was misunderstanding about proving negation or didn't apply disproving the statement by proving negation flexibly.
Suppose there is a statement that you should prove or disprove. Let's say, after the brainstorming in my head, if I figured out that the given statement is false so I have to disprove it. When disprove the statement, most of the times you negate the given statement and try to find a counterexample. If I can show a counterexample, then that is enough to prove the negation is true. If I show the negation is true, then the original statement is disproved.
Here is the statement from Quiz #6:
For all real numbers x, y, if x and y are both positive, then
Now, I want to disprove this statement, so I found the negation and showed there exists a counterexample.
Let
Let
Notice,
Then,
Then,
Therefore,
Thus,
Note that we don't need to indent anything when you show that there is a counterexample. You indent the next proof line only when you assume something. But in this case, showing negation is true, we only introduce there exists a counterexample, so we can write the each step without any indentation.
After this quiz, I realized that I didn't write some of my proofs in assignment #2. Thanks to the quiz, I could handed in the right format of proofs.
Sunday, October 26, 2014
Week 7: Quiz review
We've continued practicing proofs in the lectures. This week, I would like to review the quiz #4 because I realized that I missed important thing. Quiz #4 was writing a proof statement for the given statement.
When you show the statement is true/false, you pick a number for the part of the proof. (Ex. x, y, z). In the main part of the proof, a number I picked should be expressed as a different number from the one in the original statement. If the number's symbol was x, then I should use the number, for example, x' to indicate that this is different number. Then, when I conclude, I can use the original symbol to generalize. The below is the given statement in quiz #4.

So, basically, to prove the above statement, in the process of proving, I should have used other related symbol instead of z in the original statement. If it wasn't this quiz, I probably wouldn't realize and keep doing in a wrong way in my proof. Now, the following is the proof that I rewrote with 'the correct' symbols.
Assume x and y are real numbers. # x, y are typical generic real numbers.
Assume x > y. # antecedent.
Let z is a real number. # def'n of z'. z' is a real number st x > z and x > y.
Then, x > z'.
.
.
.
# Prove there is z' satisfies x > z'.
.
.
Then, z' > y.
.
.
.
# Prove there is z' satisfies z' > y.
.
.
Then, x > z and z' > y # by previous proofs.
Then, # since we assumed z s a real number.
# since we assumed z s a real number.
Then, # since we assumed x > y. we got this conclusion.
# since we assumed x > y. we got this conclusion.
Then, # we assumed generic real # numbers x, y.
# we assumed generic real # numbers x, y.
Sorry for the unmatched line in the last three steps of my proofs! I tried to match the line, but since I copied the equation as a picture, the size won't change. I tried to type the whole proof using LaTex but it wasn't pretty in the end. Anyway, the bottom line is that now I remember for sure to use different symbols in my main part of proof!
When you show the statement is true/false, you pick a number for the part of the proof. (Ex. x, y, z). In the main part of the proof, a number I picked should be expressed as a different number from the one in the original statement. If the number's symbol was x, then I should use the number, for example, x' to indicate that this is different number. Then, when I conclude, I can use the original symbol to generalize. The below is the given statement in quiz #4.
So, basically, to prove the above statement, in the process of proving, I should have used other related symbol instead of z in the original statement. If it wasn't this quiz, I probably wouldn't realize and keep doing in a wrong way in my proof. Now, the following is the proof that I rewrote with 'the correct' symbols.
Assume x and y are real numbers. # x, y are typical generic real numbers.
Assume x > y. # antecedent.
Let z is a real number. # def'n of z'. z' is a real number st x > z and x > y.
Then, x > z'.
.
.
.
# Prove there is z' satisfies x > z'.
.
.
Then, z' > y.
.
.
.
# Prove there is z' satisfies z' > y.
.
.
Then, x > z and z' > y # by previous proofs.
Then,
Then,
Then,
Sorry for the unmatched line in the last three steps of my proofs! I tried to match the line, but since I copied the equation as a picture, the size won't change. I tried to type the whole proof using LaTex but it wasn't pretty in the end. Anyway, the bottom line is that now I remember for sure to use different symbols in my main part of proof!
Sunday, October 19, 2014
Week 6: Proofs
The class continued how to write proofs with some different conditions such as proving inequality, existence, a sequence, non-boolean functions, using definition, proof by cases...We studied all these different cases but the structure of the proofs were basically same.
You start with the general assumption.
ex) Assume that n is generic natural number.
And then, use indentation on the next line in order to start an assumption under the initial assumption. You prove the process one in each line. At the end of each line, put '#' symbol and justify your process all the time. These assumption also need an indentation under the assumption. When you reached the last process, write the conclusion for the last assumption with the same position as the starting of the last assumption. Same thing with the other assumptions and conclusions.
ex)
Assume that n is generic natural number.
Assume that...... #explain why
Then, prove 1... #justify this proof
Then, prove 2... #justify this proof
.
.
.
.
Then, ...(conclusion), since assumed that... #assume that.....got (conclusion)
Then,......(complete conclusion), because n is generic natural number.
Above is the general format of proving example. This actually reminded me of function recipe in python. When you write a body of function definition, if we use if, for, while, etc., we have to put an indentation on the next line which is the content of those. And when it's finished and return something, unindent the line back. I understood the format of proving, but if I don't know how to prove things, it wouldn't matter. So I guess the important thing is that I practice 'how to show that something is true\false'.
Sunday, October 12, 2014
Week 5: Continued proving and Mid-term exam!
This week we had the first mid-term exam. Yes! Mid-term exam. For me, it was the very first exam since I start at U of T. I was very worried that the exam might be too hard so there's question which I can't even solve. It turned out that it wasn't a 'super-hard-I-have-no-idea' exam. Actually, I was surprised at resemblance of previous session's exam.
Before the exam, I went over all my notes, and practice tutorials, quizzes, assignment and the old exam that professor posted. I kept doing again because somehow, I felt like I have a different answer every time I tried the questions. That actually why I was so worried. I wasn't sure if I am capable of doing logic in a right way.
Since the test allowed to bring a piece of paper that I can write anything that I wanted. At first, I thought about taking some notes with me. But I decided not to take anything with me and just take the test. I thought, if I still didn't understand and don't know something until the moment I take a test, that means, I don't know. The fact that I still needs some memo on how to interpret something into logic means I still don't understand the concepts, so even though I have aids with me, that won't really help. I mean, even if I had a help sheet, when I look at the questions, if I have no idea what is going on there, then it doesn't matter if I have a help sheet or not. I simply don't know. That's why I didn't bring any help sheet with me.
Anyway, the test didn't really need any help sheet. First two questions were same type as the previous session's exam and the last one was similar to the one in the assignment 1 problem. I don't know if I received good marks, but I am just glad I was able to finish all the problems on time. (Although, we kind of went over the solution on Friday lecture, I don't quite want to think about the exam since I still have the other exams to take...)
Before the exam, I went over all my notes, and practice tutorials, quizzes, assignment and the old exam that professor posted. I kept doing again because somehow, I felt like I have a different answer every time I tried the questions. That actually why I was so worried. I wasn't sure if I am capable of doing logic in a right way.
Since the test allowed to bring a piece of paper that I can write anything that I wanted. At first, I thought about taking some notes with me. But I decided not to take anything with me and just take the test. I thought, if I still didn't understand and don't know something until the moment I take a test, that means, I don't know. The fact that I still needs some memo on how to interpret something into logic means I still don't understand the concepts, so even though I have aids with me, that won't really help. I mean, even if I had a help sheet, when I look at the questions, if I have no idea what is going on there, then it doesn't matter if I have a help sheet or not. I simply don't know. That's why I didn't bring any help sheet with me.
Anyway, the test didn't really need any help sheet. First two questions were same type as the previous session's exam and the last one was similar to the one in the assignment 1 problem. I don't know if I received good marks, but I am just glad I was able to finish all the problems on time. (Although, we kind of went over the solution on Friday lecture, I don't quite want to think about the exam since I still have the other exams to take...)
Sunday, October 5, 2014
Week 4: Mixed quantifiers, proof
In week 4, we continued with symbols and quantifiers as well as starting with proof. As previously mentioned, what we are learning in this course is same as what we learned in Calculus! course during the first and the second week.
To show that the order of quantifiers cannot be switched, there was an example with the definition of limit.











To show that the order of quantifiers cannot be switched, there was an example with the definition of limit.
The definition says that 'for all epsilon, there exist some deltas', means if I choose any epsilon, I can always find delta. But can we choose delta first(switch the order of quantifiers)? No, it will not work. If I pick a specific delta first, then my enemy can choose any delta that is out of range of delta. Than, the definition is not working anymore. Therefore, we know that the order of quantifiers matters regarding to the truth of implications.
This is, although, not always true. There are some cases that implication is not affected by the order of quantifiers. When quantifiers are elements of an ordered pair, it does not change anything. For example, below are same:
When I prove something, first, I have to convince myself why this is true. In other words, I have to understand why this is true and need to have an idea about proving steps. Next step is writing down the steps of proving. When I prove something, I have to justify my thought to convince other people who will read my proof. If I find any defects in the process, I may go back to the beginning.
Now I recall the type of proofs that I learned in Calculus! course. There are four types of proofs.
- Direct proof
- Proof by contrapositive
- Proof by contradiction
- Proof by induction
In Calculus! course, proof by induction was focused. Mathematical induction is used to prove a property holds for any natural integer. If we want to prove P(n) is true, then we assume the P(1) is true and show that if P(n) is true then P(n+1) is also true.
In CS, we start with direct proof. Most of the time, direct proof can be a very hard way to prove, When, prove directly, show each link to reach to the precedents. When we prove something like,
we use following structure:
Assume x is in X.
Assume P(x).
Then, R1(x)
C2.0 for all x in X, P(x) then R1(x)
Then, R2(x)
C2.1 for all x in X, P(x) then R2(x)
...
C2.n for all x in X, P(x) then Rn(x)
Then P(x) then Q(x)
Then for all x in X, if P(x) then Q(x)
Indentation indicates scope of assumption. This reminds me of writing definition in Python. When we write definition in Python, indentation is very important. For example, when we use if statement in the function body, if indentations is not adequate, the function is not working properly.
This way of proving is slightly different from math, so it was little uncomfortable for me to use(For example, indentation).
For this week, I remember one thing very well: chains with 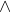 or
or 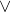 . It is because of the tutorial problem. In one of the tutorial problems, there was a question asking to write a given statement symbolically. The statement is 'A and B are both guarantees that C is true.' Actually, my answer was wrong. My answer was,
. It is because of the tutorial problem. In one of the tutorial problems, there was a question asking to write a given statement symbolically. The statement is 'A and B are both guarantees that C is true.' Actually, my answer was wrong. My answer was,
, which is not quite right. After I read this part, I could understand why my answer in not right.
Let's write the statement in symbols again. It would be
Now, following implications are equivalent to the above:
(By the rules for manipulating predicates)
Therefore,
At the time of tutorial, I didn't know what I did wrong, but after the lecture, I tried applying those rules by myself and I could understand and solve the problem.
Sunday, September 28, 2014
Week 3: continue week 2...
In this week, we continued from the week 2 contents. Followed by implication, converse and counter positive, this week, I learned about equivalence, new symbols conjunction and disjunction, more of negation, exploiting Venn Diagram and Truth Table for proving, logical arithmetic and De morgan's Law.

In both directions, the antecedents are false, so implication is true. It is odd and it looks like it is false (to me, when I instantly look at this implication), but this is equivalence.
Conjunction and disjunction is new symbols that came up on this week.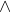 is conjunction and
is conjunction and 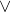 is disjunction. Conjunction meas 'and' and disjunction means 'or'. Coincidentally, they look similar to intersection and union symbols. Conjunction is used to combine two sentences into a new sentence by claiming that both of the original sentences are true. For conjunction, it is true at least one of them is true.
is disjunction. Conjunction meas 'and' and disjunction means 'or'. Coincidentally, they look similar to intersection and union symbols. Conjunction is used to combine two sentences into a new sentence by claiming that both of the original sentences are true. For conjunction, it is true at least one of them is true.
When I first saw the concept of negation, I was confused with converse. Also, I don't know why but it was hard to find negation of expressions. So when we find the negation, think about the expression that makes original implication false. For example, think about this implication 'all employees are making over 100k.' In order for this implication to be false, I need to find one (or some) employee who are making less than 100k. If the original implication is true, there will be no employee who are making less than 100k, so this would be false. Therefore, the negation is 'there exists some employees who are making less than 100k.'
We can use negation to prove that a statement is true. Because a statement will be true when its negation is false. Not only can we use negation to prove, we can also use Venn Diagram or Truth Table to prove. Venn Diagram might be hard to draw when there's more than 3 of elements to verify. In that case, we can use Truth Table to prove its truth.
Conjunction and disjunction is quite interesting. Logical arithmetic applies to these concepts just like when we calculating numbers. Also, De Morgan's Law, which I learned when I learned about sets, applies to here. This comes very useful when I try to express statements in mathematical symbols or try to interpret them.
My skill to prove or to represent statements to mathematical symbols are not really good yet. When I encounter the problems(such as tutorial problem sets), I still have to think for a good amount of time or sometimes, I can't really figure out how to answer or what kind of answer I have to give. Even though I solve the problems, I'm still not confident if this is right way to do it. I know that I can't be good at for the first attempt but sometimes it little discourages me cause I'm really not sure if I'm doing this right. When I glanced at other students' SLOGs that were posted on the course website, I could find some students who are ahead of the course. I guess the only way to be better myself is keep practicing until I am comfortable with this.
Since we had a second tutorial, I feel that the material is a lot harder. In particular, when dealing with expressing sentences into mathematical expressions , I struggle. There are some stuff that is not easy to come up with solutions and when it comes to details, I think I still need more practice. I think I was confused about existential quantifier at the beginning. However, after tutorial, it became organized in my head and now I can comprehend the problems. Although, I still have some problems to work on, I would say I generally understand the material.
When P => Q and Q => P ( P <=> Q), it is called that they are equal. There are few other ways to express equivalence:
- P iff (if and only if) Q
- P is necessary and sufficient for Q
- P => Q, and conversely
- P exactly/precisely when Q

In both directions, the antecedents are false, so implication is true. It is odd and it looks like it is false (to me, when I instantly look at this implication), but this is equivalence.
Conjunction and disjunction is new symbols that came up on this week.
When I first saw the concept of negation, I was confused with converse. Also, I don't know why but it was hard to find negation of expressions. So when we find the negation, think about the expression that makes original implication false. For example, think about this implication 'all employees are making over 100k.' In order for this implication to be false, I need to find one (or some) employee who are making less than 100k. If the original implication is true, there will be no employee who are making less than 100k, so this would be false. Therefore, the negation is 'there exists some employees who are making less than 100k.'
We can use negation to prove that a statement is true. Because a statement will be true when its negation is false. Not only can we use negation to prove, we can also use Venn Diagram or Truth Table to prove. Venn Diagram might be hard to draw when there's more than 3 of elements to verify. In that case, we can use Truth Table to prove its truth.
Conjunction and disjunction is quite interesting. Logical arithmetic applies to these concepts just like when we calculating numbers. Also, De Morgan's Law, which I learned when I learned about sets, applies to here. This comes very useful when I try to express statements in mathematical symbols or try to interpret them.
My skill to prove or to represent statements to mathematical symbols are not really good yet. When I encounter the problems(such as tutorial problem sets), I still have to think for a good amount of time or sometimes, I can't really figure out how to answer or what kind of answer I have to give. Even though I solve the problems, I'm still not confident if this is right way to do it. I know that I can't be good at for the first attempt but sometimes it little discourages me cause I'm really not sure if I'm doing this right. When I glanced at other students' SLOGs that were posted on the course website, I could find some students who are ahead of the course. I guess the only way to be better myself is keep practicing until I am comfortable with this.
∀x∈R,x2−2x+2=0⇔x>x+5∀x∈R,x2−2x+2=0⇔x>x+5
Sunday, September 21, 2014
Week 2: Quantifiers, Implication
This week, I learned about quantifiers, implication and verifying implication. This part wasn't completely surprising since it is the same contents as current Calculus class. It was helpful to have same part in two different classes at the same time. It gave me a better understanding of material.
When verify quantified claims, if it is an universal claim, show there is no 'counter-example'. In other words, if there is at least one counter-example, an universal claim becomes false. But if it is an existential claim, show there is at least one example then it is true. When there is no example, it is a false claim.
Implication is 'If P, then Q.' P is called the antecedent and Q is called the consequent. The converse of implication is 'If Q, then P.' and there is no connection between the implication and the converse. Its negation is 'If P, then not Q.' and contrapositive is 'If not Q, then not P.'
Implication can be verified in a similar manner with verifying quantified claims. Following us 'Truth Table'.
When verify quantified claims, if it is an universal claim, show there is no 'counter-example'. In other words, if there is at least one counter-example, an universal claim becomes false. But if it is an existential claim, show there is at least one example then it is true. When there is no example, it is a false claim.
Implication is 'If P, then Q.' P is called the antecedent and Q is called the consequent. The converse of implication is 'If Q, then P.' and there is no connection between the implication and the converse. Its negation is 'If P, then not Q.' and contrapositive is 'If not Q, then not P.'
Implication can be verified in a similar manner with verifying quantified claims. Following us 'Truth Table'.
P
|
Q
|
P -> Q
|
T
|
T
|
T
|
T
|
F
|
F
|
F
|
T
|
T
|
F
|
F
|
T
|
When the antecedent is false, the whole implication is true. This is because 'P' is false so it is an empty set. If it is an empty set there is no counter-example can be found. Therefore, the implication is true. When I first read this part, it was hard to accept this. What I thought is that implication should be false because 'P' is false so whole statement cannot be established. It is quite still uncomfortable but at least I understood why the implication is true when 'P' is false.
Wednesday, September 17, 2014
Week 1: Sets
In the first week of lecture, I
had a difficulty to accept the concept of 'not all' and 'not any' and I couldn't
connect the concept of building set and using boolean even though I read the material before the class. Honestly, I didn't understand the lecture right away so I could not write anything on the sheet Professor handed out.
After the lecture, I
reviewed what I learned today and try to understand the
concept step by step. When I just read the note, it wasn't clear to me what these all 'def's mean. So I decided to use examples on python. I wrote the random sets of S1, S2 in python. I tried given 'def's using True and False as elements in a set. After I tried
couple of examples, I could see the big picture and could figure out
what the comments could have been in the lecture. Following is the one example:
def q0(S1, S2):
''' (set, set) -> bool
Return whether ...
'''
return not all({x in S2 for x in S1})
It would return
'True' when all elements in S1 are not
in S2.
In other words, def q0 means:
Some elements of S1 is not an elements of S2.
At first, I was not familiar with expressions, however, after reviewing the material thoroughly it did not feel too complicated. As a result, I could solve the first week tutorial problems without having difficulties.
Subscribe to:
Comments (Atom)
